Complete Monitors for Gradual Types
Syntactic type soundness is too weak to tell apart different ways of running a program that mixes typed and untyped code. Complete monitoring is a stronger property that captures a meaningful distinction — a language satisfies complete monitoring iff it checks all interactions between typed and untyped code.
Note: this post is an extended abstract for the paper Complete Monitors for Gradual Types by Ben Greenman, Matthias Felleisen, and Christos Dimoulas. For the full paper, proofs, and slides, click here.
Example: Clickable Plot
The program below has a subtle bug. Can you find it?
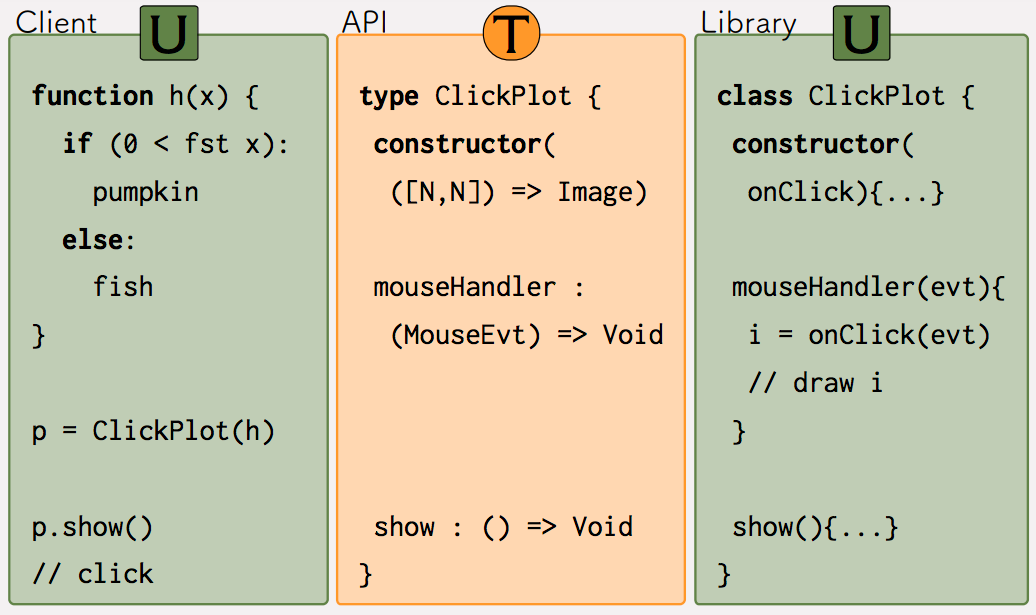
First of all, this pseudocode program combines three chunks of code:
-
On the left, an untyped client script defines a function
hthat expects a pair of numbers and returns an image. The client uses this function to create aClickPlotobject, and then displays the plot — ideally in a new GUI window. -
In the center, a typed API file describes a
ClickPlotobject as something with one constructor and two methods. The constructor expects a function; according to the type, such functions can expect a pair of numbers and must compute an image. ThemouseHandlermethod expects aMouseEvtobject and returns nothing. Theshowmethod expects no arguments and returns nothing. (Presumably, these methods have side effects.) -
On the right, an untyped library module implements a
ClickPlotobject. Most of the code is omitted (...), but themouseHandlermethod sends its input directly to theonClickcallback.
The bug is in the API — in the type ([N, N]) => Image. This type promises that a given function can expect a pair of numbers, and indeed the client function h expects a pair. But the library code on the right sends a MouseEvt object.
What happens when we run this program in a type-sound mixed-typed language? Does h receive the invalid input?
As it turns out, type soundness cannot say. A type sound language may choose to enforce or ignore the fact that the API promises a pair of numbers to the client.
Type Soundness is Not Enough
Sound types are statements about the behavior of a program. A normal type soundness theorem for a typed language says that a well-typed program can either compute a value of the same type, compute forever (diverge), or stop with an acceptable error (perhaps division by zero). No other behaviors are possible.
Classic Type Soundness
If
e : Tthen one of the following holds:
e -->* vandv : Tedivergese -->* OkError
A mixed-typed language needs two “type soundness” theorems: one for typed code and one for untyped code. The typed soundness theorem can resemble a classic theorem. The untyped soundness theorem is necessarily a weaker statement due to the lack of types:
Mixed-Typed Soundness
If
e : Tthen one of the following holds:
e -->* vandv : Tedivergese -->* OkErrorAnd if
eis untyped then one of the following holds:
e -->* vandvis an untyped valueedivergese -->* OkError
Now we can see why mixed-typed soundness is not strong enough to guarantee that the callback h in the code above receives a pair value. We have an untyped function called from an untyped context — since there are no types sitting right there, type soundness has nothing to say except that the untyped code can expect an untyped value!
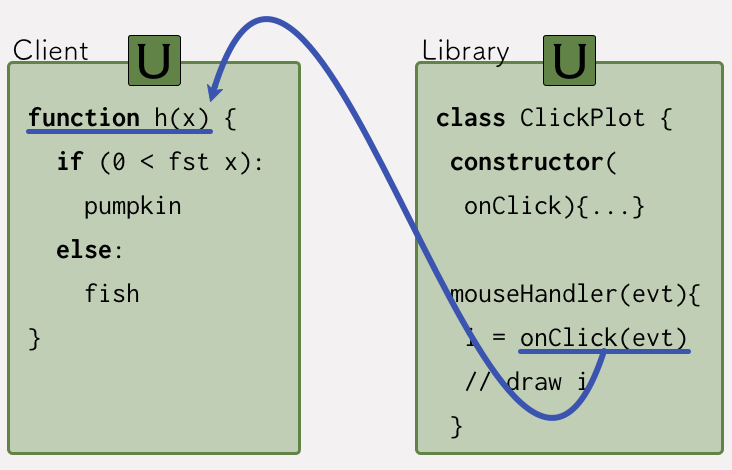
Nevertheless, this channel of communication between the library and client arose through the typed API. One might expect the type [N, N] to restrict the values that can flow across the channel; indeed, if types really are statements about the behavior of a program, then the channel needs to be protected.
The question is: what formal property separates languages thet check all typed/untyped channels of communication (whether direct or derived)? One answer is complete monitoring.
Complete Monitoring
A mixed-typed language satisfies complete monitoring iff evaluation never lets a value flow un-checked across a type boundary. To make this idea precise, we need to enrich the syntax of the language with a specification of ownership to say what parts of the program are responsible for different values, and to say how evalution changes responsibilities. Relative to a specification, complete monitoring states that every expression that arises during evaluation is made up of parts that each have a single owner.
Complete Monitoring
For all well-formed
eand alle', ife -->* e'then every subexpression ofe'has a unique owner.
This property separates our two behaviors for the Clickable Plot code. A language that satisfies complete monitoring enforces the API types with a runtime check. A language that merely satisfies type soundness may skip these checks.
An Aid to Debugging
The question raised by the Clickable Plot example is whether a language can detect one mismatch between a type and a value. A language that satisfies complete monitoring detects all such mis-matches. But we can say more. If a mismatch occurs, then programmer knows exactly where to start debugging — either the type is an incorrect specification, or the given value is flawed. In other words, complete monitoring implies a concise 2-party explanation for every type mismatch.
The paper generalizes this goal of explaining a mismatch for languages that fail to satisfy complete monitoring. There may be 2N parties to blame thanks to un-checked channels of communication, and we want to be certain to report all these parties and no false positives.
Also in the paper, you can find:
- a model of ownership, clear laws for how ownership changes during evaluation;
- examples of how to systematically add ownership to an operational semantics to attempt a proof of complete monitoring;
- definitions for blame soundness and blame completeness;
- an analysis of three semantics, which correspond to Typed Racket, Transient Reticulated, and a compromise;
- and discussion of an alternative, heap-based model of ownership.
Paper: https://www2.ccs.neu.edu/racket/pubs/oopsla19-gfd.pdf