Introducing Visual and Interactive-Syntax realized (VISr) for ClojureScript (and JavaScript)
Visual and interactive-syntax is a type of language-oriented programming that allows developers to use, view, and edit portions of a textual program with graphics. Using interactive-syntax provides the benefits of a graphical programming language, while keeping all of the benefits of a purely textual language. For example, the following is an example of a small network embedded in a program:
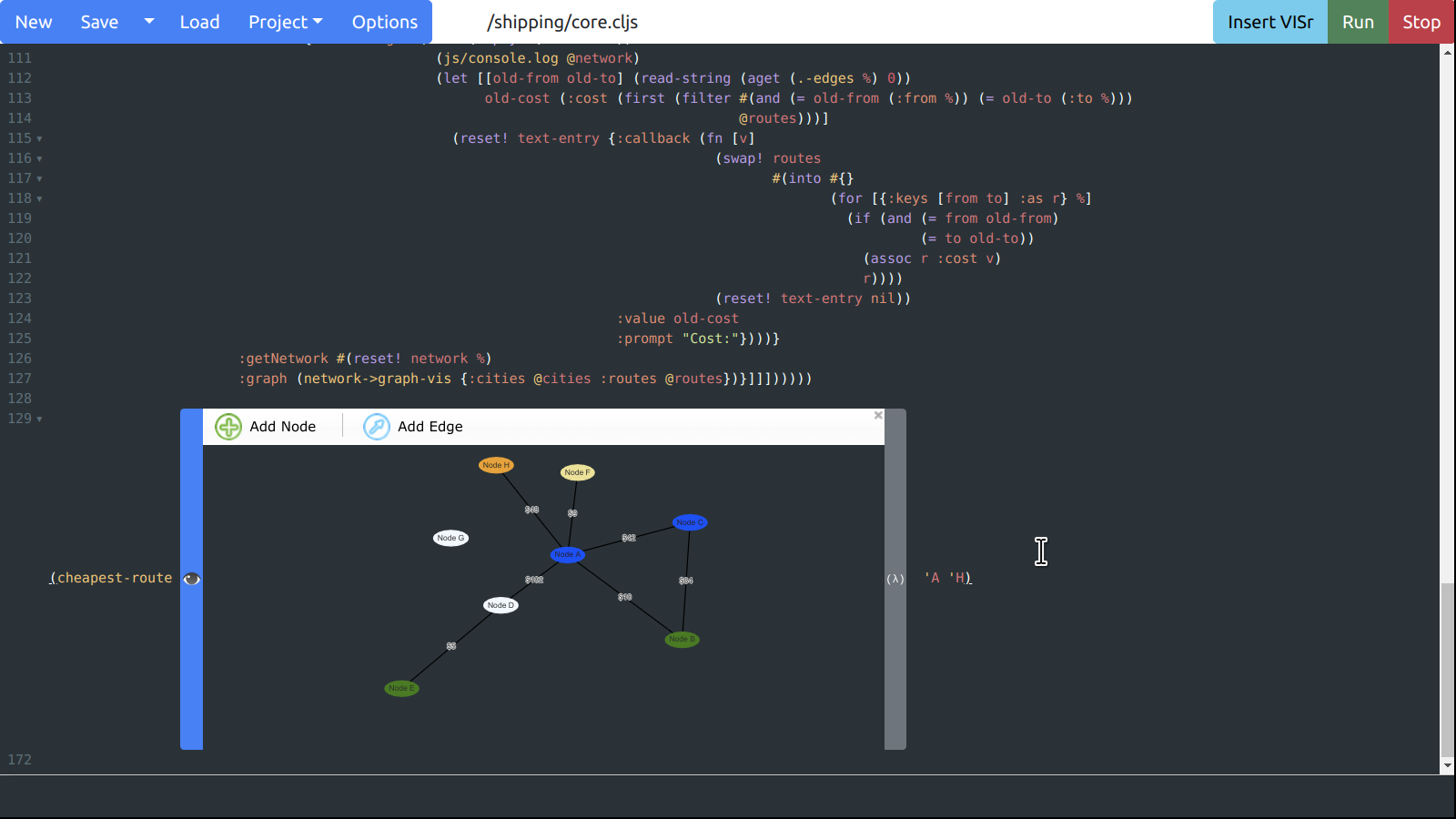
Graphical network embedded in text
Interactive-syntax is backed by human readable code; the visual components exists purely when writing and editing code. This backing means all of the tools involved in software development work with interactive-syntax extensions. For example:
- version control, such as git, works with interactive-syntax;
- programs using interactive-syntax can be written and edited with your favorite text editor or IDE;
- cut/copy/paste works with interactive-syntax using your operating system’s native clipboard;
- code analysis tools, like diff and refactor, still work with interactive-syntax; and
- you can use interactive-syntax in any language or environment that supports language-oriented programming.
To learn more about interactive-syntax, watch this video or read the accompanying paper.
VISr (Visual and Interactive-Syntax realized) for ClojureScript is a practical implementation of interactive-syntax in web browsers. The VISr environment is a full-featured IDE that supports interactive-syntax components called VISrs. Additionally, the VISr environment comes with a package manager that supports NPM packages.
This article is a brief introduction to both the VISr environment and the components that make up a VISrs. It discusses how to insert a VISr into code, how to manipulate a VISr, and how to create a new types of VISr. Future articles will discuss more advanced uses such as integrating NPM packages and using VISrs in other languages.
Deep and Shallow Types
I successfully defended my Ph.D. dissertation. You can find the document, a talk recording, and much more here:
To the PRL: thanks for a wonderful 6.5 years.
Transient for Optional and Keyword Functions
A short adventure into the depths of optional and/or keyword functions in Racket.
Transient Answers Old Questions
Several old questions from the Typed Racket mailing list have new and simple answers under a “transient” Typed Racket.
The Typed Racket Optimizer vs. Transient
What type-directed optimizations does Typed Racket perform and do any require full types?
PRL Offsite 2019 Retrospective
On November 11th 2019, the PRL had a private offsite meeting at the More Than Words bookstore in downtown Boston. For future offsite organizers, this post records what happened and how.
Complete Monitors for Gradual Types
Syntactic type soundness is too weak to tell apart different ways of running a program that mixes typed and untyped code. Complete monitoring is a stronger property that captures a meaningful distinction — a language satisfies complete monitoring iff it checks all interactions between typed and untyped code.
Four Kinds of Scoping in R
In the first and second parts of this blog series, I defined lexical and dynamic scope, and demonstrated interesting cases of scoping in R.
In this third and final part of my blog series, I’d like to discuss a paper by the creators of R, where they motivate the need for lexical scoping in a statistical programming language.
This is a “bonus” blog post, because I’m going to dive into some of the hairier R features to show how four different kinds of scoping can be simulated in R.
Scoping in R
In the previous post of this three-part blog series, we discussed lexical and dynamic scope. Now, in this second part, we can return to the original question: is R lexically or dynamically scoped?